[I originally wrote most of the piece below in preparation for an article about intrinsic information and causal composition. Ultimately, it didn’t make the cut into the final article (Albantakis and Tononi, 2019) aimed primarily at elucidating the role of causal composition within the formal framework of IIT. Nevertheless, I think the snippet here includes several noteworthy points about information in the brain, how it is typically assessed and whether it matters to the brain itself. So here you go.]
Neural networks, biological and artificial, are complex systems constituted of many interacting elements. These systems and their dynamical behavior are notoriously hard to understand, predict, and describe, due to the intricate dependencies between their parts, including nonlinearities, multi-variate interactions, and feedback loops. They also underlie many systems with specific relevance to us, including our communication networks, power grids, biological organisms, and ultimately, ourselves, that is, our brains, guiding our behavior and giving rise to our experiences. Mathematical tools for studying neural networks originate from, and are being developed within, a wide range of disciplines including information theory, computer science, machine-learning, and dynamical systems theory.
Often, the objective amounts to predicting the system’s behavior or dynamics. However, prediction neither requires a mechanistic understanding of the system under investigation, nor does it necessarily provide such an understanding (Carlson et al., 2018). A system’s behavior, for example, can often be predicted to some degree even if the system itself is treated as a black box (Figure (a)). In contrast, especially in neuroscience, characterizing the functional role of particular parts of the system (the brain) and the way in which they interact has always been a main line of inquiry.
Because the brain is commonly viewed as an “information processing” system, which receives inputs from the environment and reacts to those inputs by eliciting motor responses, information theoretical approaches seem highly appropriate for studying the functional role of the brain and its parts. More recently, also machine-learning based techniques such as “decoding” have gained popularity and have been utilized to investigate content-specific neural correlates of consciousness (Hanes, 2009; Salti et al., 2015).
The goal is to measure or identify the presence of information about some external variable or stimulus in a specific part of the brain. This part is then said to “represent” the variable or stimulus as its informational content (Rumelhart et al., 1986; Marstaller et al., 2013; Kriegeskorte and Kievit, 2013; King and Dehaene, 2014; but see Ritchie et al., 2017 for a critical discussion).
For example, the neural response of a particular brain region \(X\) may be correlated with a statistical feature \(E\) of a stimulus set presented to the subject, which can be quantified by the mutual information \(I(E;X)\) (Figure (b)). By contrast, decoding approaches aim to infer a particular stimulus or stimulus feature \(E = e_{t-1}\) presented to the subject from the subsequently recorded neural response \(X = x_t\) (Figure (c)).
[Recently, researchers have also begun to employ similar approaches in order to gain a better understanding of artificial neural networks (information theory, e.g.: Schwartz-Ziv and Tishby, 2017; Tax et al., 2017; Yu et al., 2018; causal information: Mattsson et al., 2020; and machine-learning, e.g.: Lundberg and Lee, 2017).]
While neurons are typically viewed as the units of information processing, the brain is also functionally compartmentalized at the level of macroscopic brain regions. An important insight from early applications of decoding techniques to neurophysiological and neuroimaging data is that populations of neurons (Pouget et al., 2000; Panzeri et al., 2015) and patterns of fMRI voxels (Haxby et al., 2001) can contain additional information compared to individual neurons or voxels. Current neural decoding approaches thus focus on multivariate approaches, such as multivariate pattern analysis (MVPA) (Haynes, 2011; Haxby et al., 2014), or also representational similarity analysis (RSA) (Kriegeskorte and Kievit, 2013), based on the underlying assumption of a “population code”.
Panels (a-c) in the figure below summarize the current techniques used in complex system science, and neuroscience in particular, that we have reviewed above.
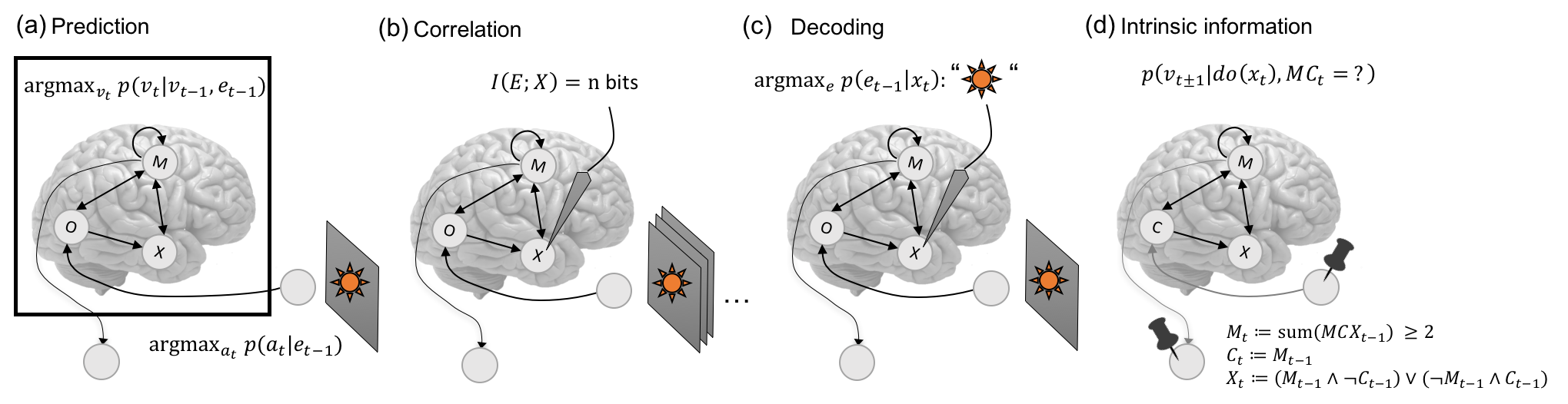Figure: Extrinsic and intrinsic information. Extrinsic information is correlational, based on observational data, and typically relates a system’s actions or internal states with states of the environment. (a) Predicting a future action \(a_t\) or internal state \(v_t\) of the system. Predictive information about the most likely action \(a_t\) of a system can be obtained based on the stimuli \(e_{t-1}\) it receives from the environment while treating the system as a black-box (indicated by the black line). Alternatively, future system states \(v_t\) can be predicted based on observational data of past system states \(v_{t-1}\) and inputs to the system \(e_{t-1}\). (b) Positive mutual information between external variables \(E\) and system subsets (e.g., \(X\)) is often taken as an indicator of the presence of external information in the respective part of the system. (c) While mutual information quantifies correlations between variables, decoders aim to infer features of the input stimuli from system subsets in a state-dependent manner. (d) Intrinsic information is causal, based on interventional data, and evaluates what the current state of the various parts of a system specify about its past and future states in a compositional manner. External variables are taken as fixed background conditions but are not further considered otherwise. See (Albantakis and Tononi, 2019) for details on the toy model system and computation.
However…
… the information that is decodable from the brain is not necessarily used by the brain itself (Haynes, 2009; Weichwald et al., 2015; Carlson et al., 2018). This is because the notion of information that is evaluated is still correlational or predictive, and thus detached from neural mechanisms. More explicitly, the fact that a stimulus feature correlates with a statistical property of the neural (population) response does not imply that this property plays a causal role within the brain (Victor 2006; Weichwald et al., 2015). Particularly in the case of information decoded from multiple variables (neurons, voxels, or also temporal patterns), it generally remains unknown whether a mechanism exists within the brain that is capable of “reading out” the decoded information. This issue is widely recognized for nonlinear decoding techniques, which are deemed “more powerful” decoders than the brain itself (see, e.g., Naselaris et al., 2011; King and Dehaene, 2014).
[The maximal amount of “Shannon” information about a visual stimulus, for example, is present in the retina and can only decrease down the processing pipeline (Cox, 2014) by the Data processing inequality. Any external feature in the input can thus, in principle, be decoded from the retina, although the retina itself clearly lacks the necessary mechanistic structure to “process” or “read out” this information.]
Linear classifiers, however, are commonly considered “biologically plausible approximation[s] of what the brain itself does when decoding its own signals” (from Ritchie et al., 2017; see, e.g., DiCarlo and Cox, 2007; King and Dehaene, 2014). Yet, even linear decoders may extract correlational information from specific brain regions that is not causally relevant to the brain itself (Williams et al., 2007; Ritchie et al., 2017; Carlson et al., 2018). On the other hand, neurons—the units of information processing—have nonlinear (integrate-to-threshold) input-output functions (Koch and Segev, 2000), and also at larger scales, nonlinear processes may still play a significant role in shaping the brain’s dynamics (Heitmann and Breakspear, 2018). Moreover, MVPA applied to sets of fMRI voxels may fail to decode information that can be retrieved from single-unit data from the same brain area (Dubois et al., 2015). Taken together, also linear classifiers may both over- and underestimate the information that plays a causal role within the brain (or other neural networks).
To sum up, understanding a complex system such as the brain requires more than successful prediction (see also Kay, 2018). However, neither standard information-theoretical, nor decoding-based approaches can ultimately capture the causal role of the parts of the system. This is because these techniques are based on observation and correlation with external variables. They evaluate the information present in the system from the perspective of an external observer. They do not determine whether the system itself possesses the necessary mechanisms to “read out” its own “messages”. Information processing requires processors, decoding requires decoders. Yet, what counts as a mechanism, information processor, or decoder from the perspective of the system itself remains poorly understood.
What is needed, is an account of intrinsic information that explicitly acknowledges the limited perspective of the system itself but also captures the information specified by all of the system’s components. One such account of intrinsic information and intrinsic mechanisms is offered within the formal framework of integrated information theory (IIT) (see Figure (d)). While above I have focused on the functional role of neural components within the brain, the problem with extrinsic notions of information also arises for consciousness and its contents. IIT’s account of intrinsic information is causal and compositional: it unfolds the full intrinsic causal structure of a system. But rather than diving into specifics now, I will leave you with a few references that highlight our recent efforts towards a principled account of intrinsic information:
Barbosa et al. (2020) discuss that standard information measures are not suited to capture information from the perspective of a part within the system, even in the context of quantifying information transmission, and proposes a novel and unique measure of intrinsic information.
Haun and Tononi (2019) provide a first demonstration of how the content of experience (here, the feeling of spatial extendedness) could be captured by the intrinsic causal structure of a particular model system—an account of how meaning could be generated from within.
Finally, my FQXi essay on the topic of intrinsic information provides more background on necessary conditions for intrinsic information and meaning from the IIT perspective (Albantakis, 2018).